Понятия абстрактных алгебраических объектов (групп, полей, колец, а также и других, которые здесь не рассматриваются) возникли в математике исследовании общих свойств операций сложения и умножения.

1. Основные определения и примеры.

Определение 1. Множество G, снабженное операций "*", условно называемой умножением, называется группой, если операция обладает следующими свойствами: 

1) для любых трех элементов выполняется равенство f * (g * h) = (f * g) * h (ассоциативность);

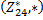2) существует такой элемент , что  для любого  (существование единицы);

3) для любого элемента  существует такой элемент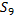, что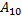 (существование обратного элемента).

Группа называется коммутативной (или абелевой), если 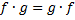 для всех .

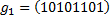Подмножество 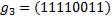 называется подгруппой в G, если из  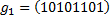следует, что .

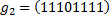Очевидно, если множество H - подгруппа, то оно само является группой.

Определение 2. Отображение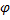:  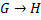группы G в группу H называется гомоморфизмом, если  для всех 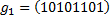. Гомоморфизм называется эпиморфизмом, если он является сюръекцией, и мономорфизмом, если он - инъекция. Если гомоморфизм является одновременно и эпиморфизмом, и мономорфизмом, то он называется изоморфизмом. Группы, между которыми существует изоморфизм, называются изоморфными, и с алгебраической точки зрения они неразличимы.

Определение 3. Множество R, наделенное операциями сложения "+" и умножения "*", называется кольцом, если эти операции обладают следующими свойствами:

1) для любых элементов a и b ϵ R имеет место равенство a + b = b + a (сложение коммутативно);

2) если c ϵ R, то (a + b) + c = a + (b + c) (сложение ассоциативно);

3) существует такой элемент 0 ϵ R, что 0 + a = a + 0 = a для любого a ϵ R (существование нуля);

4) для любого a ϵ R существует такой элемент -a ϵ R, что (-a) + a = a + (-a) = 0 (существование противоположного элемента);

5) для любых элементов a, b и c ϵ R выполняются равенства